MMI:Maximum Mutual Information
1. 背景
在传统的seq2seq领域,多样性问题一直是个令人困扰的问题,一个典型的例子就是bot领域,在回答的时候容易生成一些非常safe,grammatical的reply,比如“呵呵”,“I don’t know”之类,这些回答可以顺应人们的问题,但是基本没有太多实际的意义,试想,谁会使用一个问啥都说不知道的bot呢。
针对这个问题,有很多相关的研究,比如模型派倾向于通过复杂精妙的模型来提升diversity,也有一些研究倾向于在损失函数领域作出有效调整,本篇论文便是损失函数领域的工作。
尽管seq2seq有着需要专业领域知识少,可以端到端训练,可以学习到source sentence与target sentence之间的语义和句法信息等优势,不过,它也有只建模source->target的单向关系,而忽略了target->source的依赖关系的劣势,而反向依赖在phrase-based的模型上有着良好的表现,所以,如果可以为seq2seq模型加入这个信息,模型的能力应该会有比较好的提升。
基于这样的想法,作者提出在seq2seq中引入双向关系,并通过最大化互信息来改善seq2seq的效果。
2. 互信息
在概率论和信息论中,两个随机变量的互信息(mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。互信息是点间互信息(PMI)的期望值。互信息最常用的单位是bit。
一般地,两个离散随机变量 X 和 Y 的互信息可以定义为:
其中 p(x, y) 是 X 和 Y 的联合概率分布函数,而 

其中 p(x, y) 当前是 X 和 Y 的联合概率密度函数,而 

上面的公式不够直观,可以进行如下的化简: \(\begin{align}I(X;Y) &= \int_{Y}\int_{X}p(x,y)log(\frac{p(x,y)}{p(x)p(y)})dxdy\\&=\int_{Y}\int_{X}p(x.y)log(\frac{p(x,y)}{p(x)})dxdy-\int_{Y}\int_{X}p(x,y)log(p(y))dxdy\\&=\int_{Y}\int_{X}p(x)p(y|x)log(p(y|x))dxdy-\int_{Y}log(p(y))\int_{X}p(x,y)dxdy\\&=\int_{X}p(x)\int_{Y}p(y|x)log(p(y|x))dxdy-\int_{Y}p(y)log(p(y))dxdy\\&=H(Y)-H(Y|X)\end{align}\) 直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y 共享:知道 X 决定 Y 的值,反之亦然。因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的熵。而且,这个互信息与 X 的熵和 Y 的熵相同。(这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。)
3.流程
论文主要通过3步来实现:
-
使用普通的seq2seq或者attention-seq2seq来分别训练$p(x y)$和$p(y x)$ -
通过$p(y x)$生成N-best 列表 该列表通过beam search来生成,不过作者在实验中发现,标准的beam search算法生成的N-best 列表多样性欠佳,N个句子的主要区别就是标点符号或者一些小的形态变化,生成的word的重叠率很高。作者的解释是标准的beam search算法只探索了搜索空间的一小部分。
为了解决这个问题,作者提出了一种针对beam search的改进:
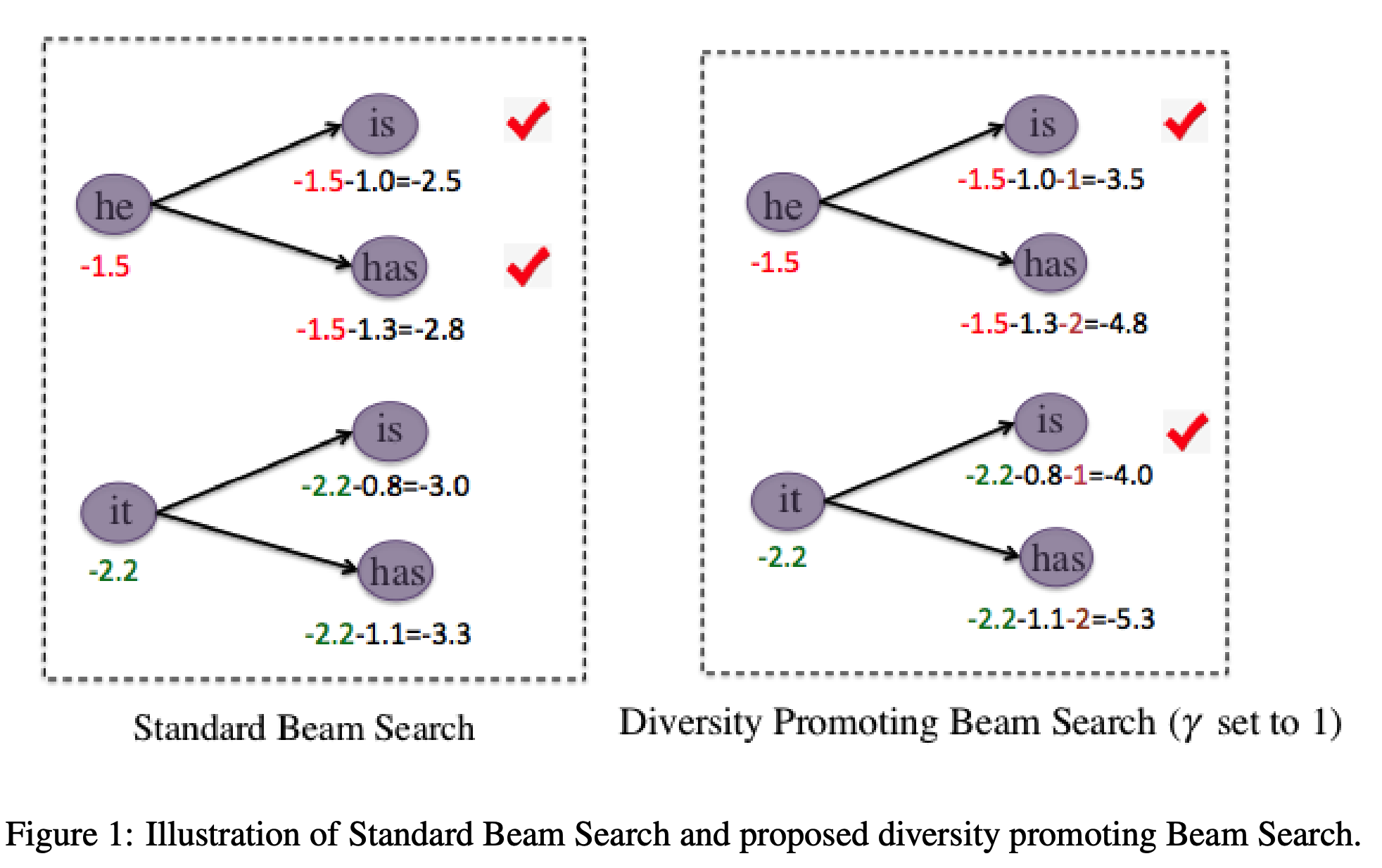
以上图为例,在生成token的时候使用标准的beam search,但是在选择的时候减去衰减系数$\gamma k$,具体做法是针对同一个token产生的后续序列,比如图中的he,对其score进行重排序,然后对一个预测的token减去其排序号,比如he预测的is排第一(即k=1),那么减去$\gamma k$为1,has同理。这样的话针对同一个token产生后续token,排在底部的token会被惩罚,这样的惩罚以后,其他的token产生的序列便可能浮上来,如“it is”,这便增加了N-best列表的多样性。
-
通过线性添加$p(x y)$来重排N-best 列表 生成多样性的N-best列表以后,重点就是reranking工作了,即如何从这些候选sentence中选出最好的句子,这个选择过程通过混合$log (p(x y))$和$log(p(y x))$来实现,source的得分可以通过1中训练的$p(x y)$来计算。 除了考虑$log(p(y|x))$,作者也考虑了$log(p(y))$,即在target这个单语语料库上训练出来的语言模型概率,此外,作者也考虑了将target的长度$L_{T}$加入loss中,最终整合成如下的打分函数,来对每个句子进行打分: \(score(y) = log p(y|x) + \lambda log p(x|y)+\gamma log p(y)+\eta L_{T}\) 通过优化$\lambda$,$\gamma$,$\eta$来实现选句。

