memory network
1. 背景
记忆网络是一种最早提出于2014年的网络,这个网络与seq2seq有许多相似之处,不过有其特殊之处,该网络经过几年的发展,已经发展出了不少的新技术,本篇文章讲话对该类网络进行个较为详细的介绍。
2. 方法历程
2.1 memory networks
这个网络提出的背景是基于大部分的机器学习模型不能读和写一个long-term memory component的部分内容,并能与inference无缝结合,这种缺陷使得他们无法良好利用现代计算机的资源。
传统的深度学习模型(RNN、LSTM、GRU等)使用hidden states或者Attention机制作为他们的记忆功能,但是这种方法产生的记忆太小了,无法精确记录一段话中所表达的全部内容,也就是在将输入编码成dense vectors的时候丢失了很多信息。所以本文就提出了一种可读写的外部记忆模块,并将其和inference组件联合训练,最终得到一个可以被灵活操作的记忆模块
一个memory network有一个memory m(对象数组,比如vector array,strings array等等)和4个components I,G,O,R组成:
- I:(input feature map) 将输入转换成内部feature representation
- G:(generalization) 利用新的输入更新旧的memories
- O:(output feature map) 给定新输入和新的memory state的情况下,生成feature representation space下的新的输出
- R:(response) 将输出转化成期待的响应格式,比如文本响应或一个action
给定输入x(可以是字符,数字,图片等等),模型的流程如下:
-
把x转换成内部feature representation I(x).
这里可以选择特征特征方式,比如bag of words,RNN encoder states, etc.
-
使用新输入I(x)更新memories $m_{i}$:$m_{i}=G(m_{i},I(x),m),\quad \forall(i)$
将输入句子的特征 x 保存到下一个合适的地址
,可以简单的寻找下一个空闲地址,也可以使用新的信息更新之前的记忆 简单的函数如
,H(x) 是一个寻址函数(slot choosing function),G 更新的是 m 的 index,可以直接把新的输入 I(x) 保存到下一个空闲的地址
,并不更新原有的 memory,当然更复杂的 G 函数可以去更新更早的 memory 甚至是所有的 memory
-
利用新输入和memory计算输出特征 o:$o=O(I(x),m)$
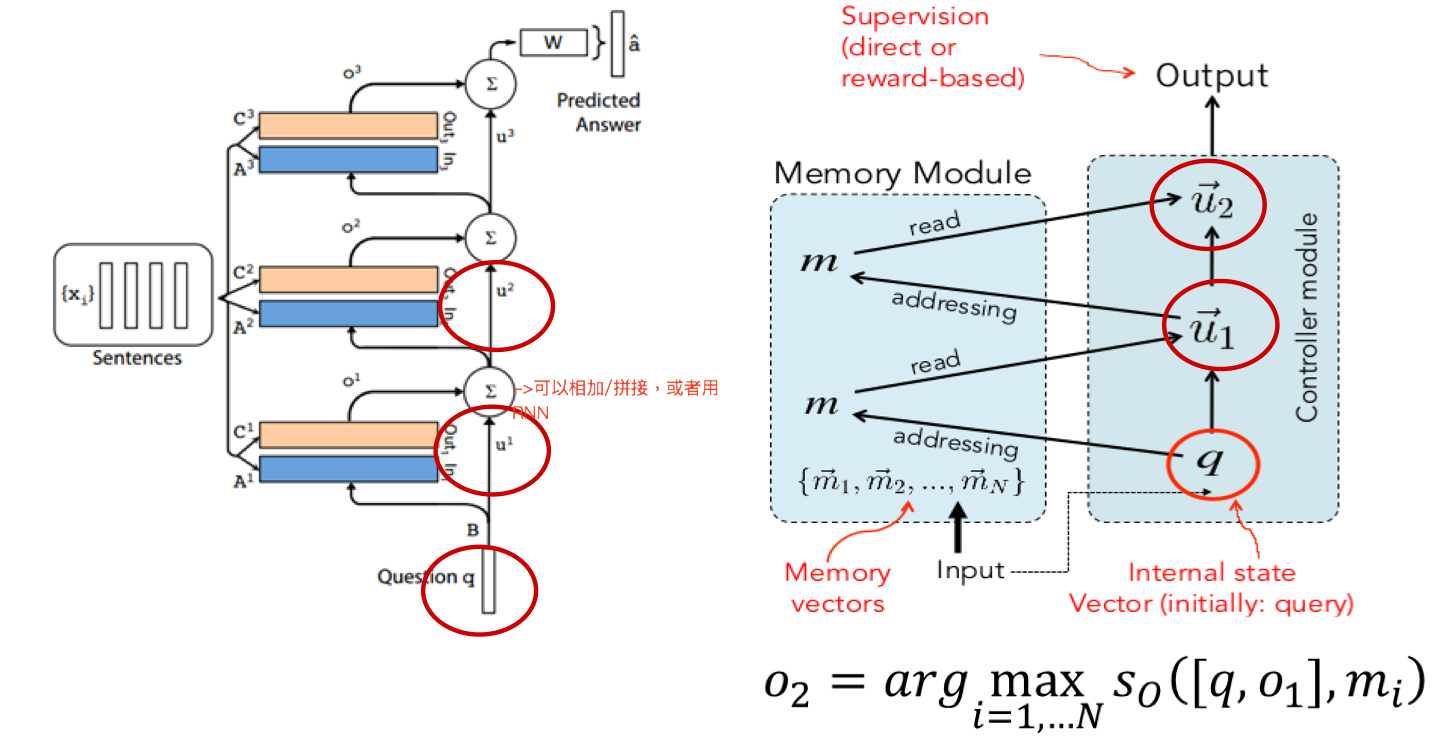
寻址,给定 query Q,在 memory 里寻找相关的包含答案的记忆
: 问题 q 和事实 m 的相关程度,当然这里的 q,m 都是特征向量,可以用同一套参数也可以用不同的参数 U:bilinear regression 参数,相关事实的
分数高于不相关事实的分数
n 条记忆就有 n 条 bilinear regression score 回答一个问题可能需要寻找多个相关事实,先根据 query 定位到第一条最相关的记忆,再用第一条 fact 和 query 通过加总或拼接等方式得到 u1 然后一起定位第二条
-
将输出特征o编码为最终的响应:$r=R(o)$
将 output 转化为自然语言的 response
可以挑选并返回一个单词比如说 playground 在词汇表上做一个 softmax 然后选最有可能出现的单词做 response,也可以使用 RNNLM 产生一个包含回复信息的句子,不过要求训练数据的答案就是完整的句子,比如说 football is on the playground
train和test都遵循这个流程,不同的是,test的时候只存储memories而不更新模型参数。
上面的介绍是个提纲挈领的介绍,说明了memory network的一般设计流程,而具体的模型实现则在后续的研究中给出。
2.2 End-To-End Memory Networks
这篇论文提出了一种不同于2.1节的一种memory network,它引入了一个循环注意力网络,并实现了端到端的训练。该模型接收一组要存储于memory中的离散输入$x_{1},…,x_{n}$,一个query q,然后输出一个answer a。其中,每个$x_{i}$,q,a包含的符号均来自于一个 字典,容量为V。模型将每个x以固定的size写入到memory中,然后计算x和q的一个连续representation,这个representation会通过多个hops用于后续求a。
接下来会详细介绍该模型。
2.1.1 Single Layer
该结构实现了一个memory hop操作,具体为:
-
Input memory representation
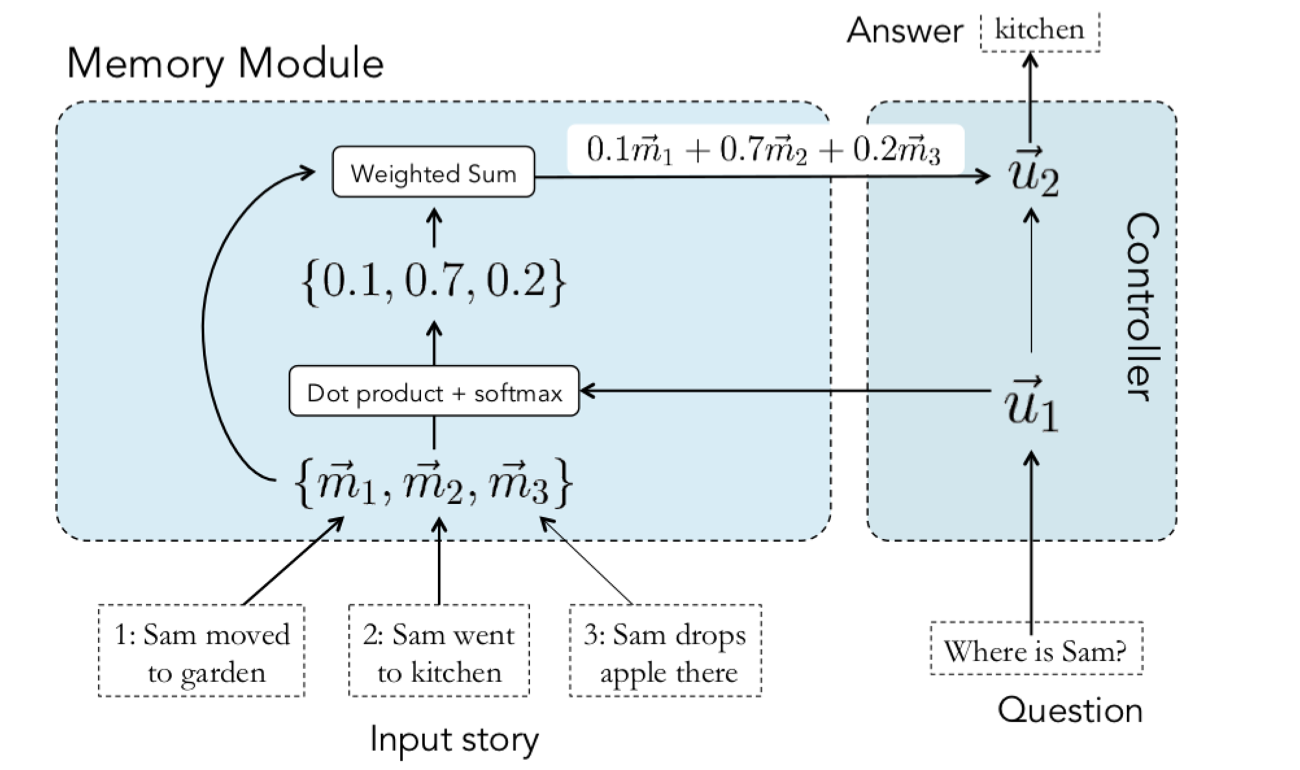
对于给定的输入集合$x_{1},…,x_{n}$,通过将每个$x_{i}$ embedding到一个连续空间把$x_{i}$转化为memory vector $m_{i}$,维度为d,最简单的情况就是使用一个embedding矩阵 A,维度为$d \times V$,query q也被embeded(同样可以采用另一个embedding矩阵B表示,维度同A)来获得一个内部状态$\mu$,通过内积并后接softmax来计算$\mu$和$m_{i}$的匹配程度: \(p_{i}=Softmax(\mu ^{T}m_{i})\)
-
Output memory representation
每个$x_{i}$都有个对应的输出向量$c_{i}$(可以用另一个embedding 矩阵C),来自于memory o的响应向量通过如下方式计算: \(o=\sum_{i}p_{i}c_{i}\) 由于输入到输出的函数是平滑的,所以可以很自然的使用bp算法优化。
-
Generating the final prediction
预测的label通过如下方式计算: \(\hat a= Softmax(W(o+\mu))\)
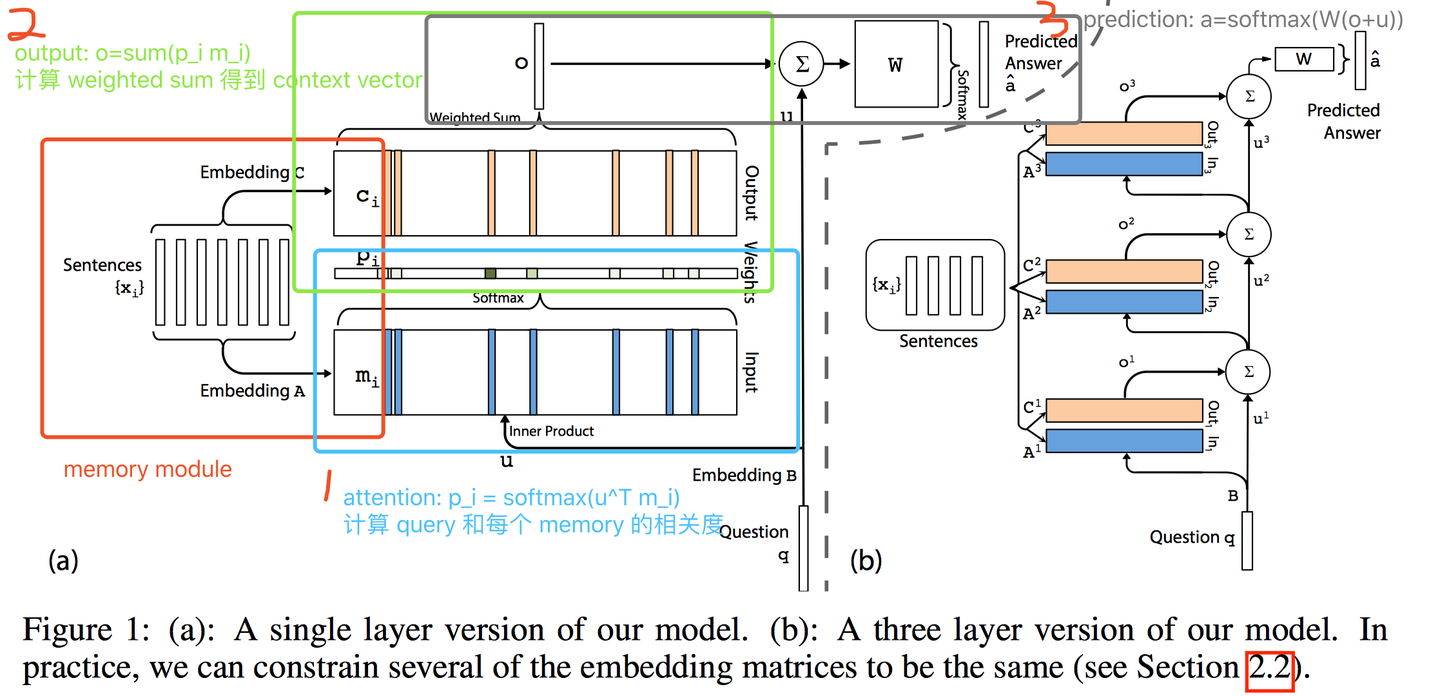
2.1.2 Multiple Layers
多层(K)结构堆积方式如下:
-
高层(>=2)的输入为:$\mu ^{k+1}=o^{k}+\mu^{k}$
-
每一层都有自己的embedding 矩阵$A^{k},C^{k}$
这里作者探索了两种方式:
Adjacent
前一层的输出是这一层的输入
$W^{T}=C^{K}$;
Layer-wise(RNN-like)
不同层之间用同样的 embedding
可以在 hop 之间加一层线性变换 H 来更新
-
模型顶层输出为:$\hat {a}=Softmax(Wu^{k+1})=Softmax(W(\mu^{k}+o^{k}))$
2.3 Dynamic Memory Networks(DMN)
该网络提出于2016年,论文的提出是为了解决QA(question answer)问题:
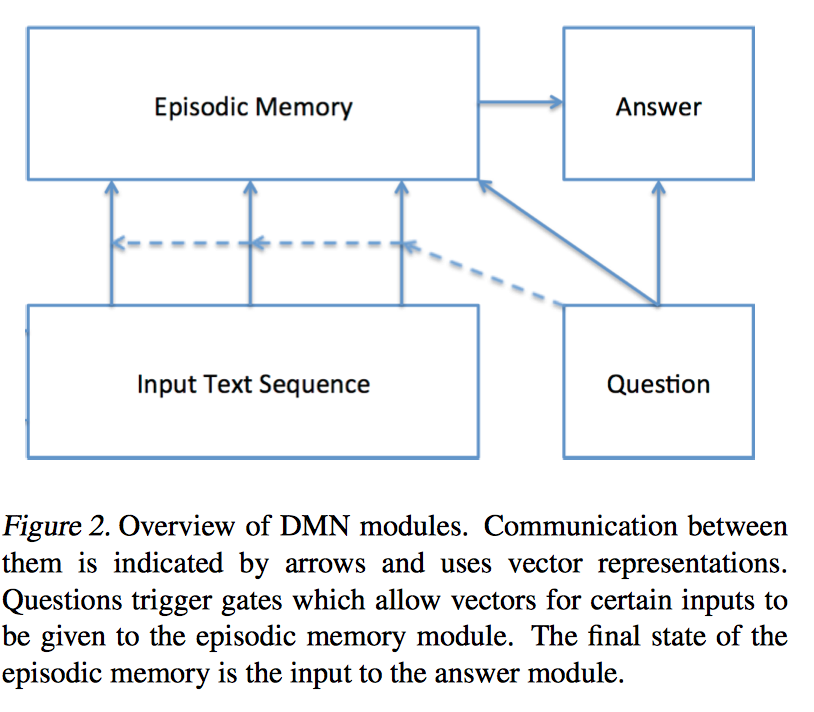
从图中可以看到,DMN可以分为四个部分:
-
Input Module
该模块将原始的文本输入编码成向量,这个可以使用常用的RNN实现,论文中作者使用的是Gru。生成长度为$T_{c}$ fact representation c。
输入可以是一个/多个句子,一篇/几篇文章,包含语境信息和知识库等,使用 RNN 进行 encoding,每一个句子编码成固定维度的 state vector。 具体做法是把句子拼到一起(每个句子结尾加标记符 EOS),用 GRU-RNN 进行编码,如果是单个句子,就输出每个词的 hidden state,$T_{c}$为句子中单词的数目;如果是多个句子,就输出每个句子 EOS 标记对应的 hidden state,$T_{c}$为句子的条数
-
Question Module
该模块将问题编码成向量q,该模块同样使用Gru,对于一个有$T_{Q}$个单词的question,使用Gru的最终的hidden state作为输出。
该模块的embedding矩阵可以与Input module共享。
-
Episodic Memory Module
该模块一般可以通过一个带有attention机制的GRU实现。在给定输入文本向量集合c的情况下,该模块通过attention机制决定应该关注哪些输入向量,然后根据问题向量q和以前的“memory”产生一个新的“memory”向量$e^{i}$。在每次迭代的过程中,该模块都能有效抽取输入的相关信息,并更新自己内部的episodic memory:$m^{i}=GRU(e^{i},m^{i-1})$,初始状态使用问题向量q来初始化:$m^{0}=q$。
论文中以QA为例子介绍了该模块的细节,因为QA涉及到多个fact,所以对这类任务有个对输入进行多轮次处理(multiple passes)的需求,见下图,因为对于每个question,需要通过多轮的处理才能总结出多个fact句子的逻辑联系,比如,当被问及“where is the football?”的时候,第一轮迭代应该关注句子7:“John put down the football.”,因为该句子涉及到了football关键词,当模型看到john与问题相关的时候它才能在第二轮迭代的时候获取John在哪里的信息,第二次找到第 6 个句子 John went to the hallway,第三次找到第 2 个句子 John moved to the bedroom。最终在迭代$T_{M}$passes后,最终的memory $m^{T_{M}}$会被送入answer module。(感觉上该模块类似于于HRED模型中的context RNN,通过句子级的RNN实现多个句子context的建模)
Attention Mechanism
一般attention机制均涉及到计算输入向量集合权重的问题,在该模型中也是这样,权重计算方式为:$g_{t}^{i}=G(c_{t},m_{t-1},q) $
其中G为gating function, 论文中使用两层的前向神经网络实现。在某些数据集,比如Facebook’s bAbI 数据集上,会有一个标量表明哪个fact与question更重要,因而在这些数据集上,可以通过有监督的方式训练G,t代表input module中第t个位置上的fact representation。
Memory Update Mechanism
该机制是为了计算pass i的episode,方式为使用GRU处理fact representation c,其中每个$c_{t}$乘以$g^{i}$权重,最终输出给answer module的是该GRU的最终的hidden state,该GRU的处理与普通的GRU略有不同,使用如下公式更新时间步t的hidden state以及计算episode: \(h_{t}^{i}=g_{t}^{i}GRU(c_{t},h_{t-1}^{i})+(1-g_{t}^{i}h_{t-1}^{i})\)
\[e^{i}=\left\{\begin{matrix} h_{T_{c}}^{i}\quad other \\ h_{t}^{i} \quad sequence \ modeling\ task \end{matrix}\right.\]Criteria for Stopping
由于该模块也是基于GRU的,因而也需要设定什么时候终止迭代。作者通过在输入中增加了一个特殊的end-of-passes representation来终止迭代。对于没有显示监督信息的数据集,设定一个最大的迭代次数。
-
Answer Module
利用memory module产生的最终memory 向量生成答案。根据任务的不同,该模块会在episodic memory迭代结束后或者在每个时间步出发。
该模块同样适用GRU实现,初始状态为$a_{0}=m^{T_{M}}$,在每个时间步,用问题向量q,上个hidden state $a_{t-1}$,以及上个预测的输出$y_{t-1}$生成本次预测和更新本次状态: \(y_{t}=softmax(W^{(a)}a_{t})\)
\[a_{t}=GRU([y_{t-1},q],a_{t-1})\]$[y_{t-1},q]$代表拼接上个产生的词和问题向量,同时使用cross-entropy训练。

通过上面的介绍可以发现,DMN模型涉及到了5个GRU的训练,可以说是非常复杂了,也比较难以训练。
2.4 DMN+
该模型同样提出于2016年,主要是针对DMN的一些缺陷进行了改进,其结构基本与DMN相同,模块部分略有改动,因而主要看一下其改动。
-
Input Module的问题
DMN模型在一些有 supporting facts(the facts that are relevant for answering a particular question)信息的数据集上表现良好,不过在没有supporting facts的数据集上表现并没有多好,作者认为是GRU只能获取来自它前面的句子的信息,而不能活去到后面句子的信息,这 1. 会阻断来自未来句子的信息传递 2.只用 word level 的 GRU,很难记忆远距离 supporting sentences 之间的信息
-
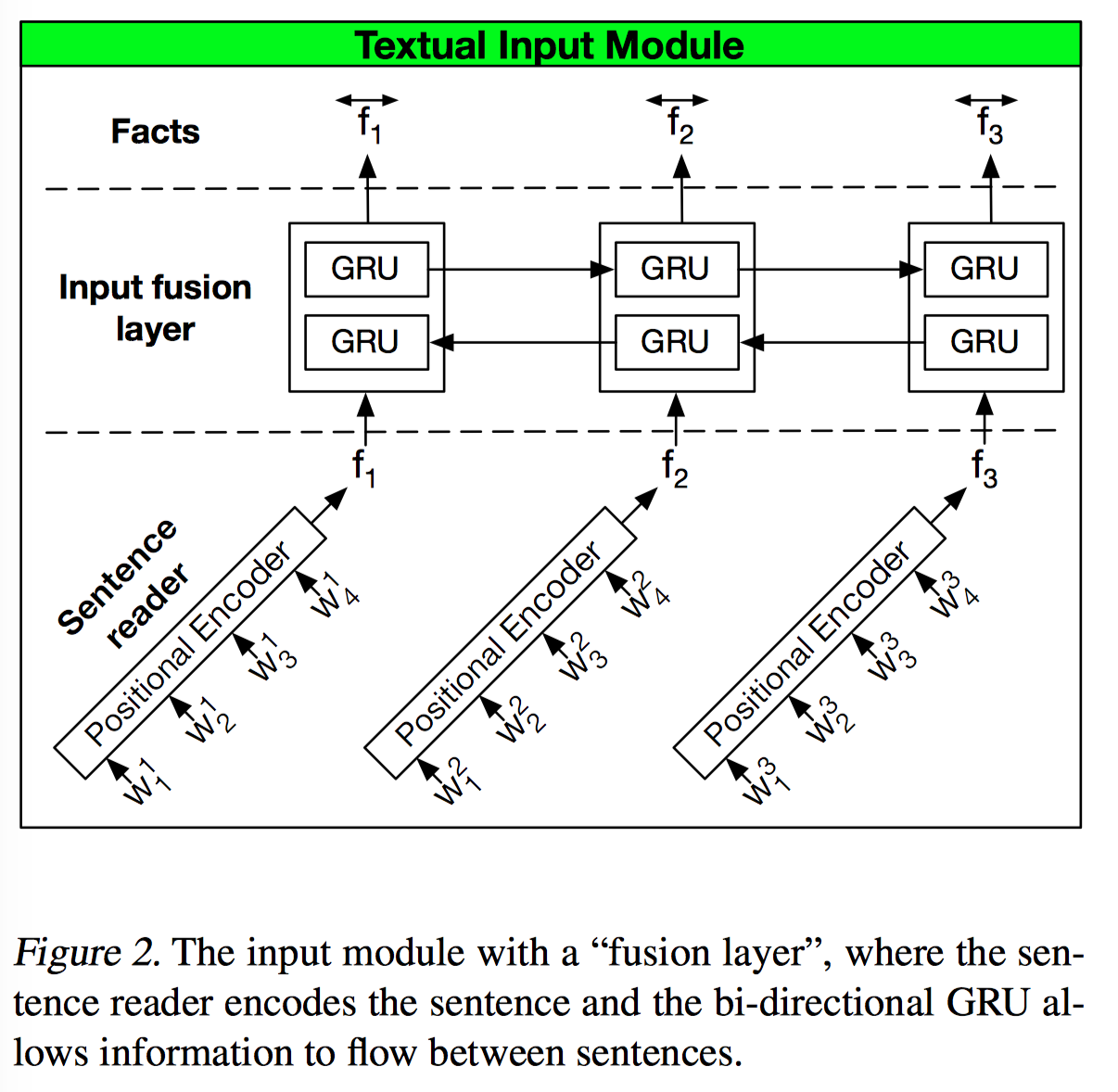
Input Fusion Layer
针对Input Module的问题,作者提出了使用两个不同的组件来替换单个GRU。
sentence reader
第一个组件,负责将句子进行embedding,这里使用positional encoder(这里是因为数据集过小的原因,使用RNN容易过拟合,更好的做法是使用RNN)。
input fusion layer
进行句子之间信息交叉,从而可以实现句子之间的内容相互作用。这里可以使用双向GRU实现,这种结构可以兼顾过去和未来的信息,最终的输出为双向信息的加和。
-
Episodic Memory Module
DMN中计算权重使用的是supporting fact,不过这只适用于提供了supporting fact的数据集,对于没有该标注信息的数据集则没啥用,为了改善这一状态,DMN+使用了一种新的策略来计算attention权重: \(\begin{aligned} & z_{i}^{t}=[\overleftrightarrow{f_{i}} \circ q;\overleftrightarrow{f_{i}} \circ m^{t-1};|\overleftrightarrow{f_{i}} - q |; |\overleftrightarrow{f_{i}}-m^{t-1}|] \\ & Z_{i}^{t}=W^{(2)}tanh(W^{(1)}z_{i}^{t}+b^{(1)}) + b^{(2)} \\& g_{i}^{t}=\frac {exp(Z_{i}^{t})}{\sum _{k=1}^{M_{i}}exp(Z_{k}^{t})} \end{aligned}\) 其中,$\overleftrightarrow{f_{i}}$是第i个fact,$m^{t-1}$是上个episode memory, q是问题向量,$\circ$是element-wise乘积,$|\cdot|$是element-wise绝对值,“;”代表向量的concatenation,$M_{i}$为句子数或者句子中单词数。
对比DMN可以发现,z缺失了几项,因为作者通过分析以后发现那些多余的项是无用的。还有一点就是这里不在需要supporting fact了。同时,这里的attention计算方式也更符合普通意义上的attention。
Attention Mechanism
探究了两种方法:
soft attention:对于facts的简单加权求和,但是会丢失位置和顺序信息,不够有效。
Attention based GRU:GRU能更好的使用facts的位置和顺序等时序信息,但是它不能利用attention weight $g_{i}^{t}$,所以这里使用了一个修改的GRU:
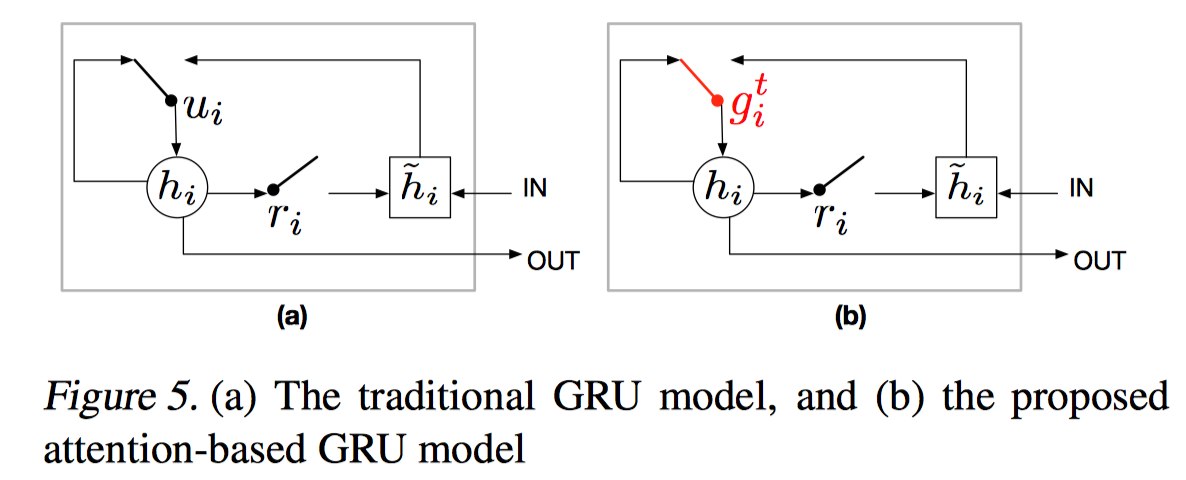
更形式化的讲是GRU的内部更新状态:
\(h_{i}=\mu_{i}\cdot \tilde{h_{i}}+(1-\mu_{i}) \cdot h_{i-1} \mapsto h_{i}=g_{i}^{t}\cdot \tilde{h_{i}}+(1-g_{i}^{t}) \cdot h_{i-1}\)
即将传统GRU的update gate $\mu_{i}$替换成了 attention 的输出 ,这样 gate 就包含了 question 和前一个 episode memory 的知识,更好的决定了把多少 state 信息传递给下一个 RNN cell。同时这也大大简化了 DMN 版本的 context 计算,因为$\mu_{i}$是向量,而$g_{i}^{t}$为标量。
context vector 是 GRU 的 final hidden state。
-
Episode Memory Updates
DMN 中 memory 更新采用以 q 向量为初始隐层状态的 GRU 进行更新,用同一套权重,这里替换成了一层 ReLU 层,实际上简化了模型。
其中 ; 表示拼接,这能进一步提高近 0.5% 的准确率。