transformer变体

1. Introduction

 在这篇博客，我们详细的介绍了transformer的结构，也介绍了transformer还存在的问题，接着本篇文章将会介绍关于transformer的多种改进，让我们了解一下更加丰富多彩的transformer结构。

2.各种变体

2.1 Universal transformers(UT)

 提出于2018年，是transformer的后续工作，它的提出是为了解决transformer固有的非图灵完备性及缺少conditional computation的问题。

 UT与transformer的结构基本相同，只是在细节方面存在着差异:

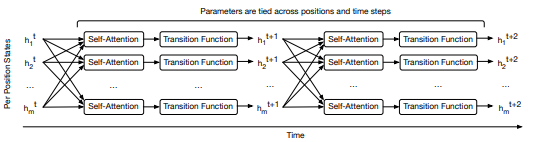
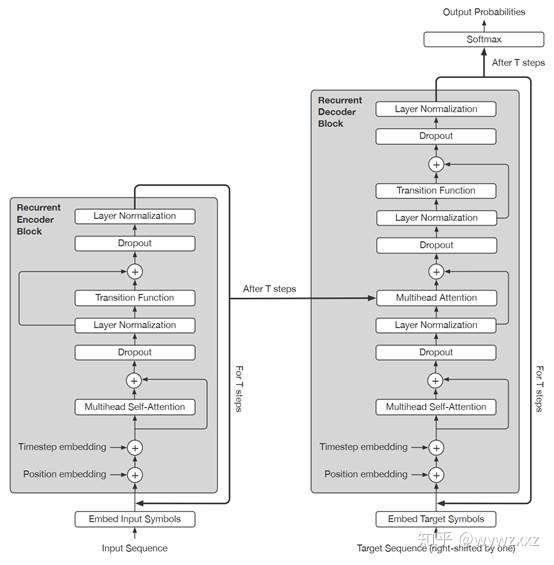
 理解transformer后这里很容易理解，稍微的区别就是注意由于transformer只有一次前传，所以位置与时间编码都是一次的，而UT则使用了类似RNN的循环，所以每次迭代都要编码位置信息和时间信息，编码方式为： \(P_{i,2j}^{t} =sin(i/10000^{2j/d})+sin(t/10000^{2j/d})\)

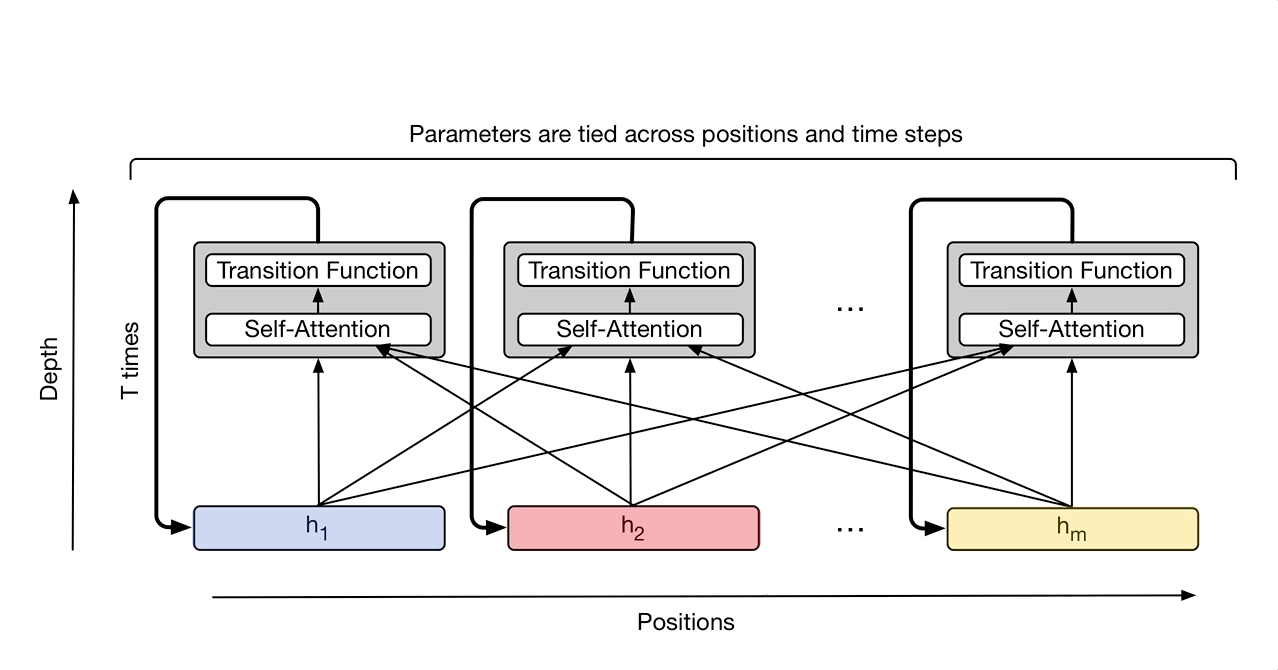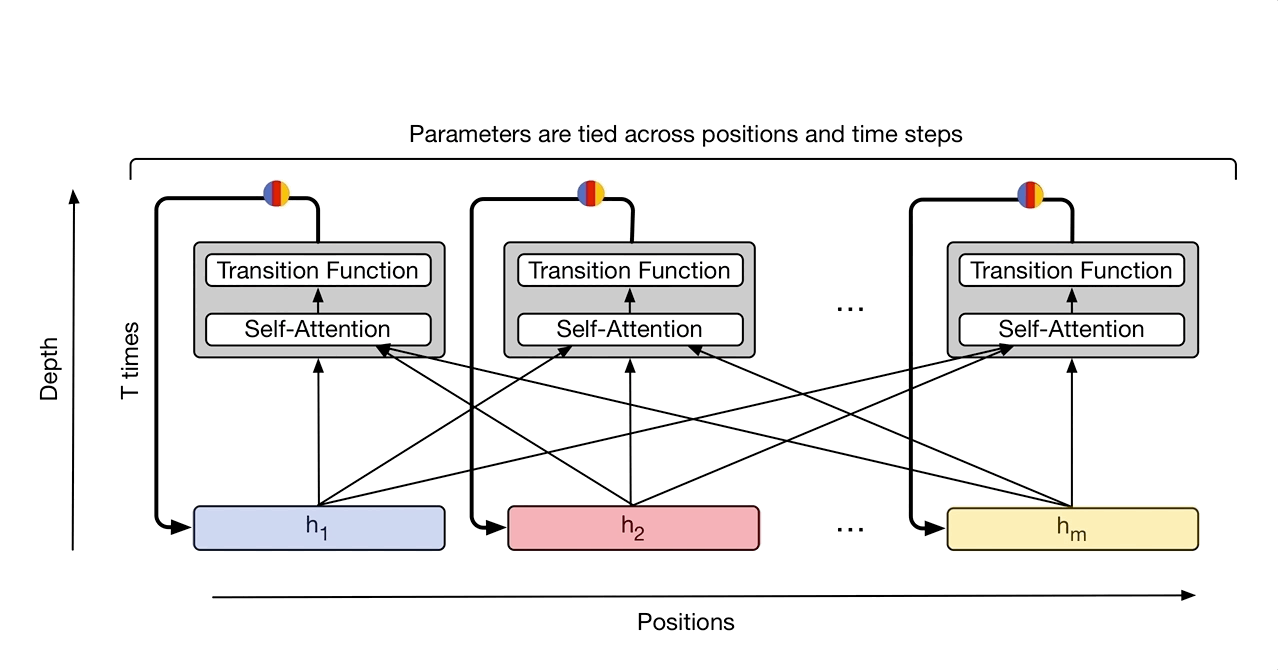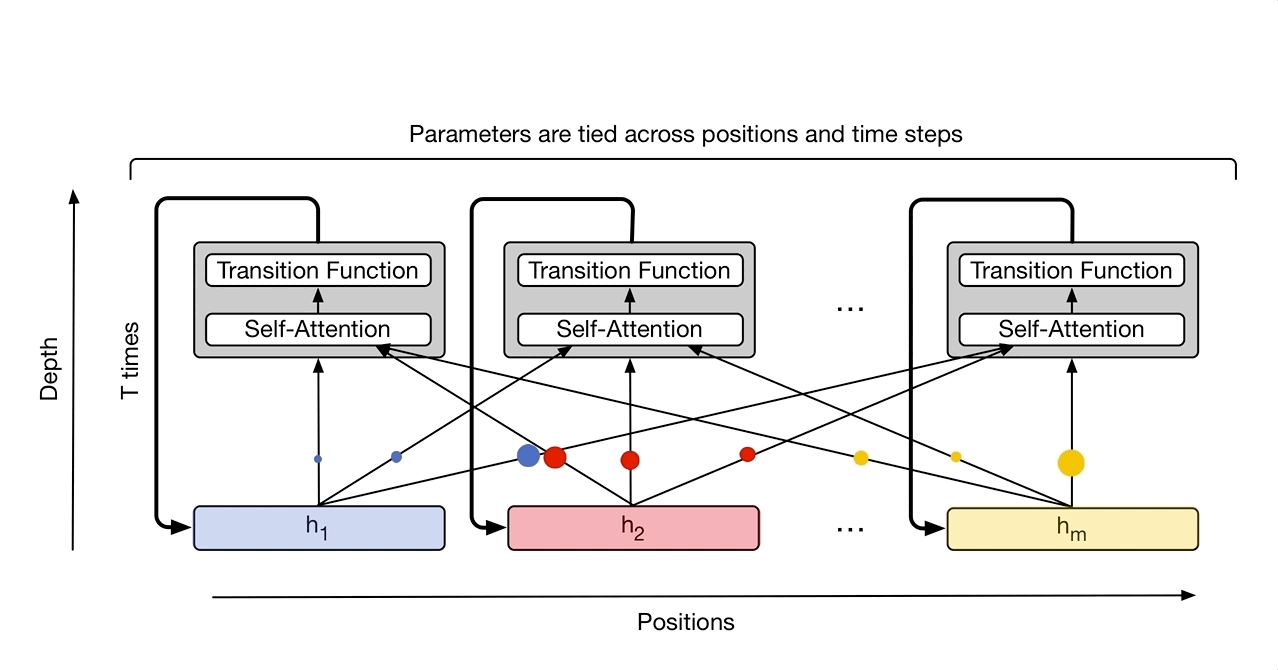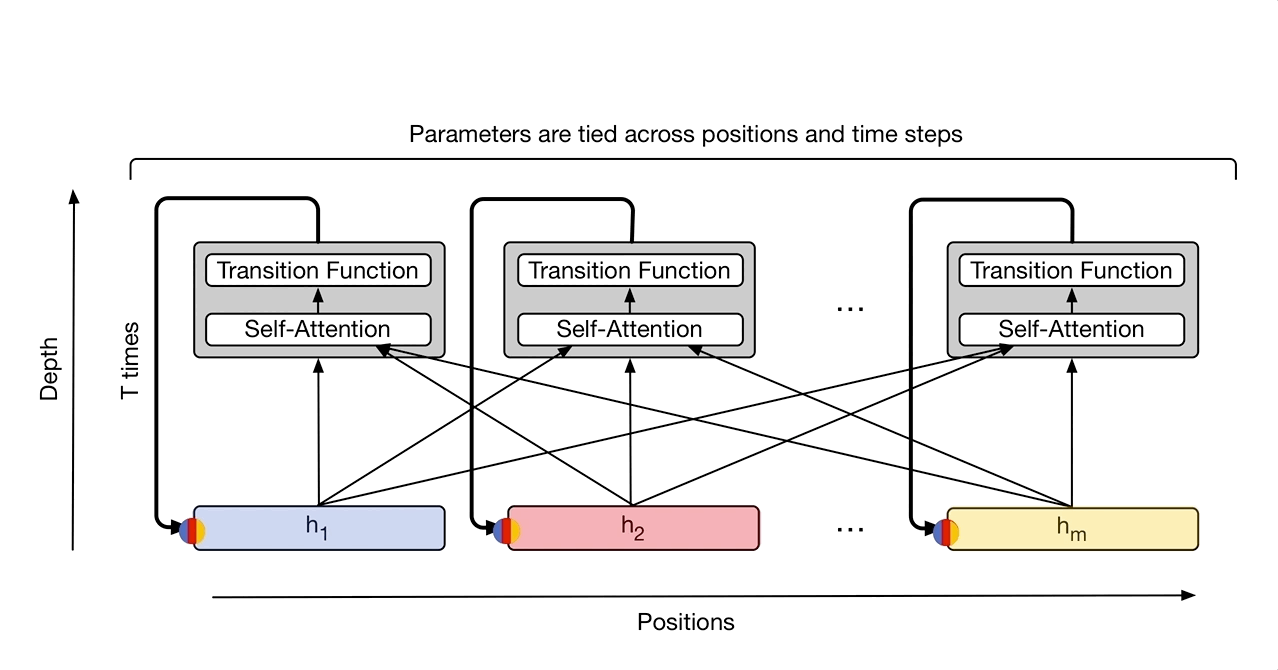
 循环的加入解决了图灵完备性问题，那么conditional computation问题则是通过Adaptive Computation Time（ACT）机制来实现的。此处供参考

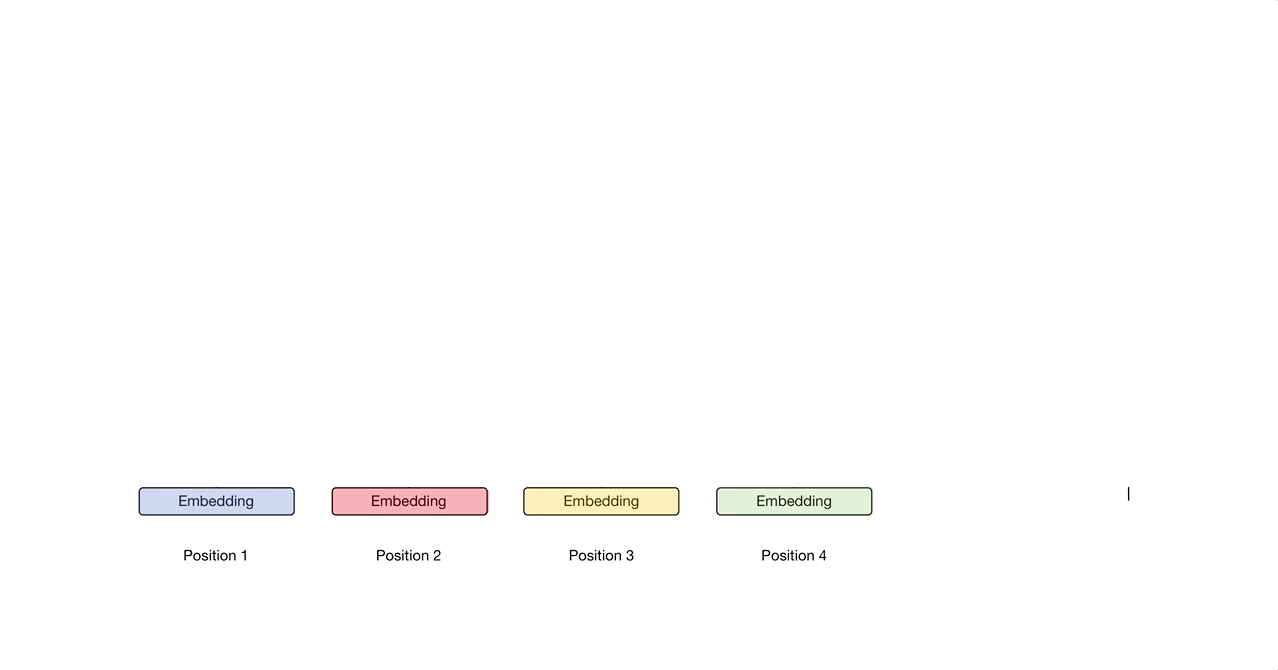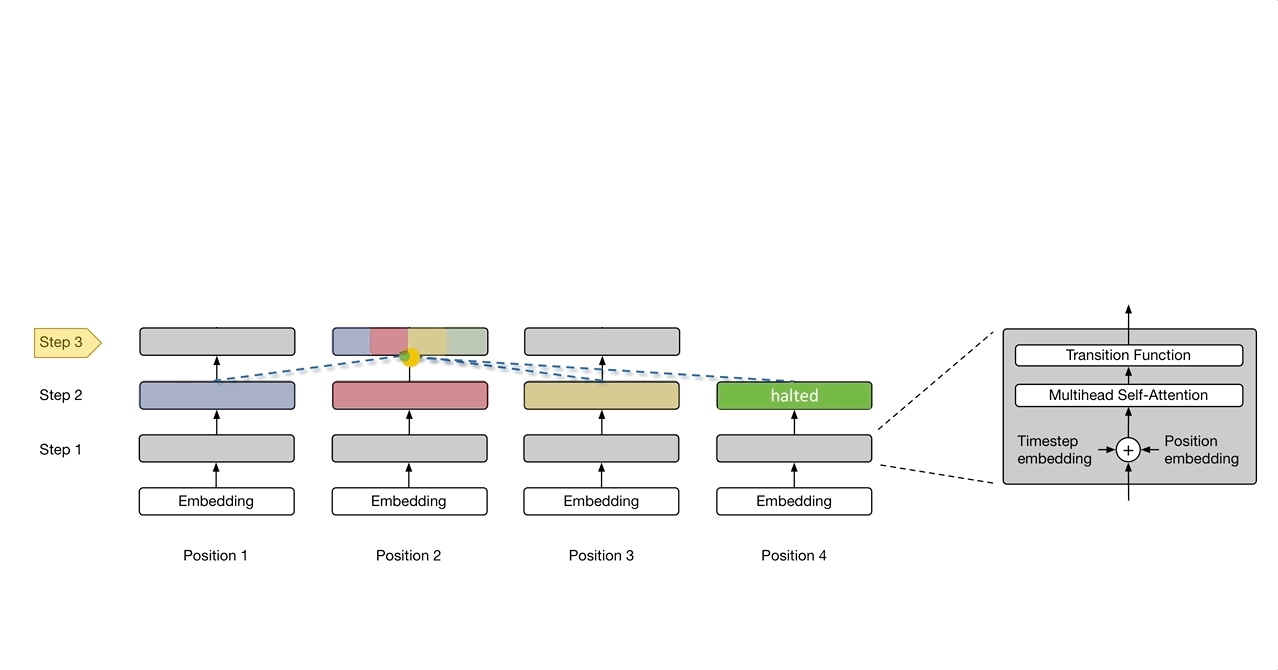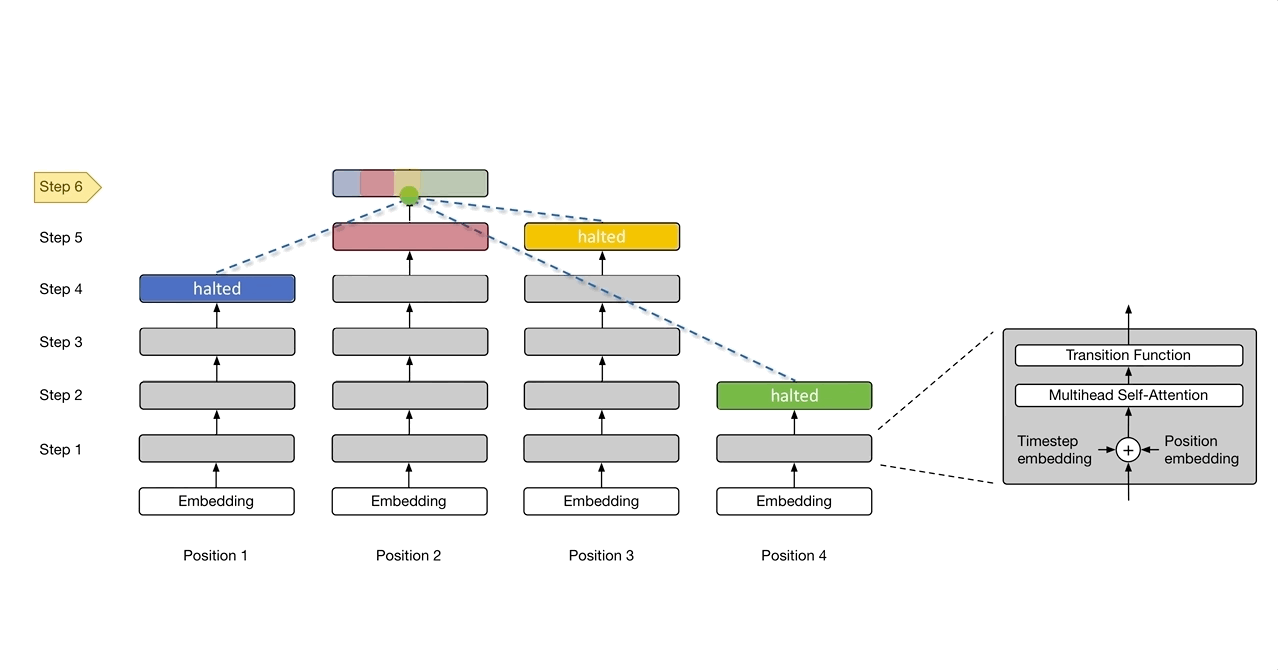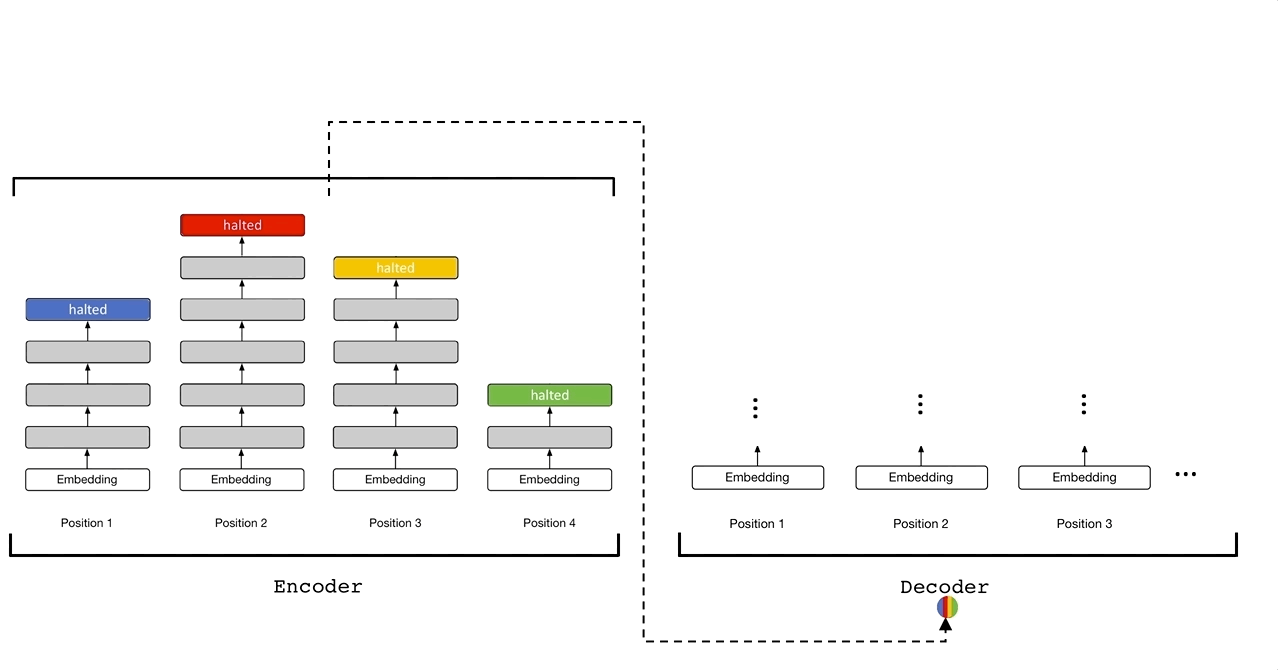
2.2 Transformer-XL

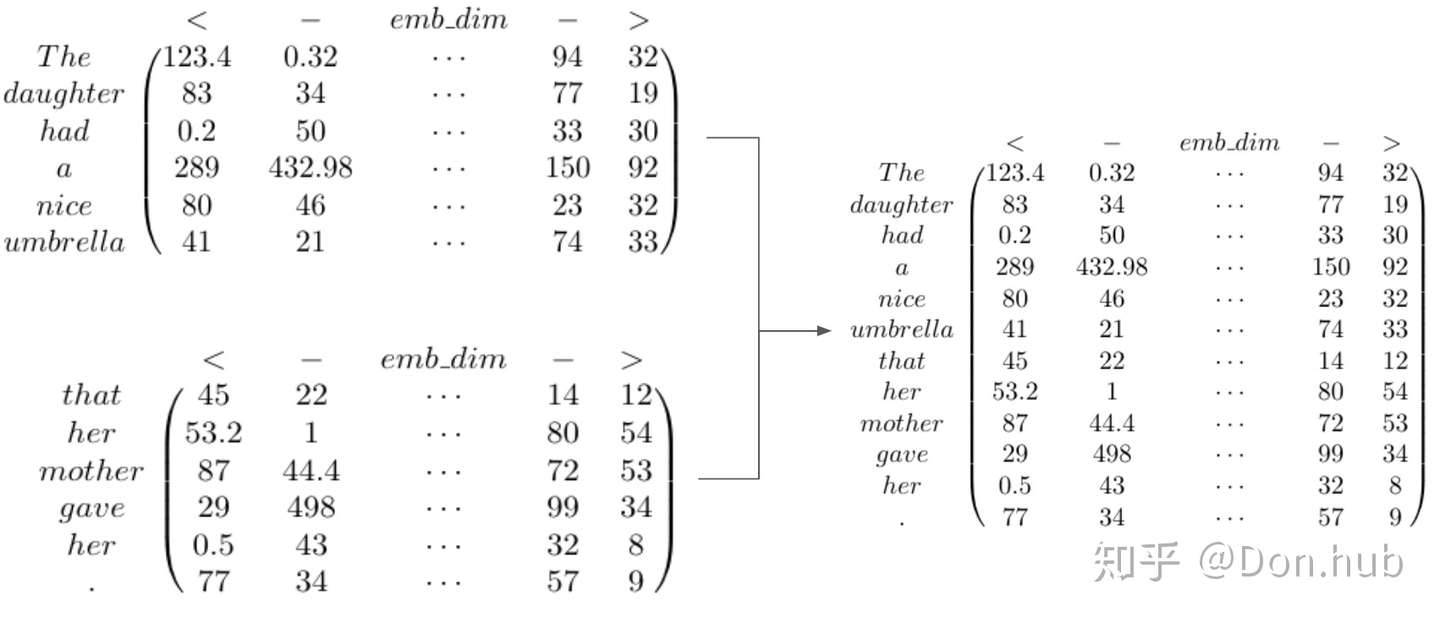
 CMU联合Google Brain在2019年1月推出的新模型，它的提出解决了transformer模型对长文本建模能力不足的问题。受限于算力问题，对于长文本，如果一次全部输入，考虑到query，key, value的shape为[batch_size, seq_len, d_model]，很容易就OOM，这时候，一个变通方法就是通过分割成长度小于等于$d_{model}$(默认512)的segment，每个segment单独处理，互不干涉，这种模型也被称为vanilla Transformer。

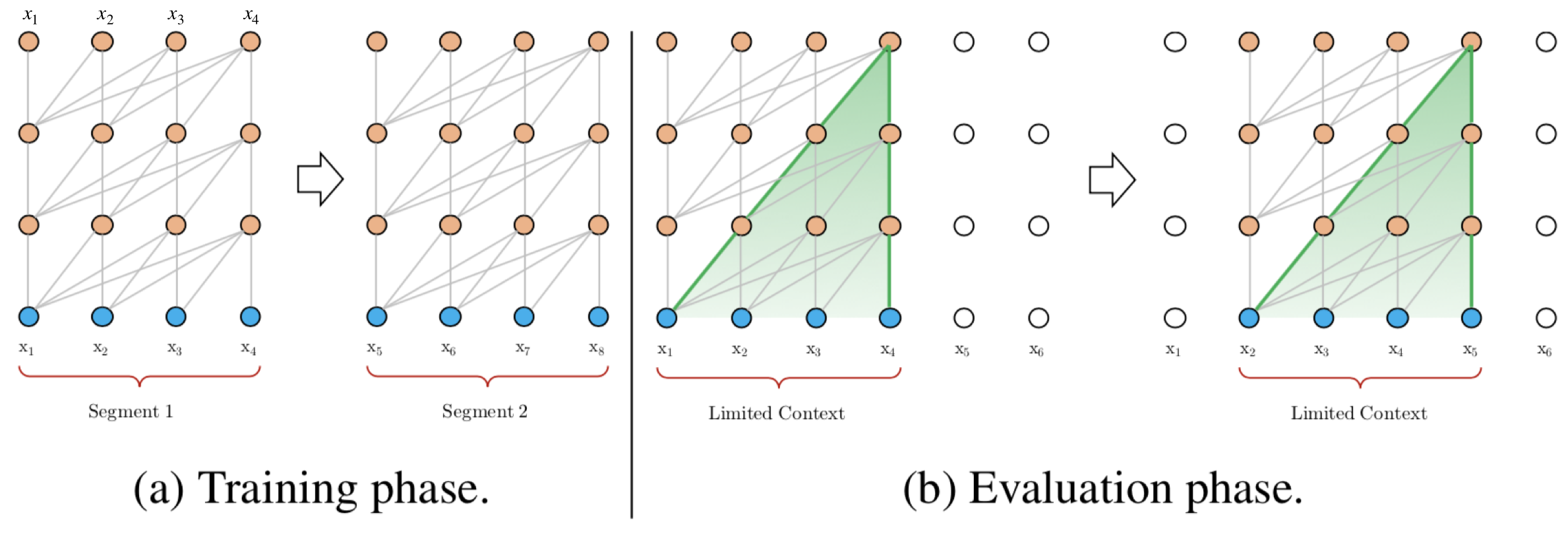
 在vanilla transformer中，根据之前的字符预测片段中的下一个字符。例如，它使用$x_{1}$ , $x_{2}$ , . . . ,$x_{n − 1}$预测字符$x_{n}$，而在之$x_{n}$后的序列则被mask掉。它将输入分成段，并分别从每个段中进行学习，如上图所示。 在测试阶段如需处理较长的输入，该模型会在每一步中将输入向右移动一个字符，以此实现对单个字符的预测。

 很显然，这样的处理是存在问题的：

1. 上下文长度受限：字符之间的最大依赖距离受输入长度的限制，模型看不到出现在几个句子之前的单词。
2. 上下文碎片：对于长度超过512个字符的文本，都是从头开始单独训练的。段与段之间没有上下文依赖性，会让训练效率低下，也会影响模型的性能。
3. 推理速度慢：在测试阶段，每次预测下一个单词，都需要重新构建一遍上下文，并从头开始计算，这样的计算速度非常慢。

 针对上面的问题，transformer-xl通过一种被称为Segment-level Recurrence的技术来解决，其思路类似于RNN，通过将前一个segment的memory送入到下一阶段来实现信息传递。

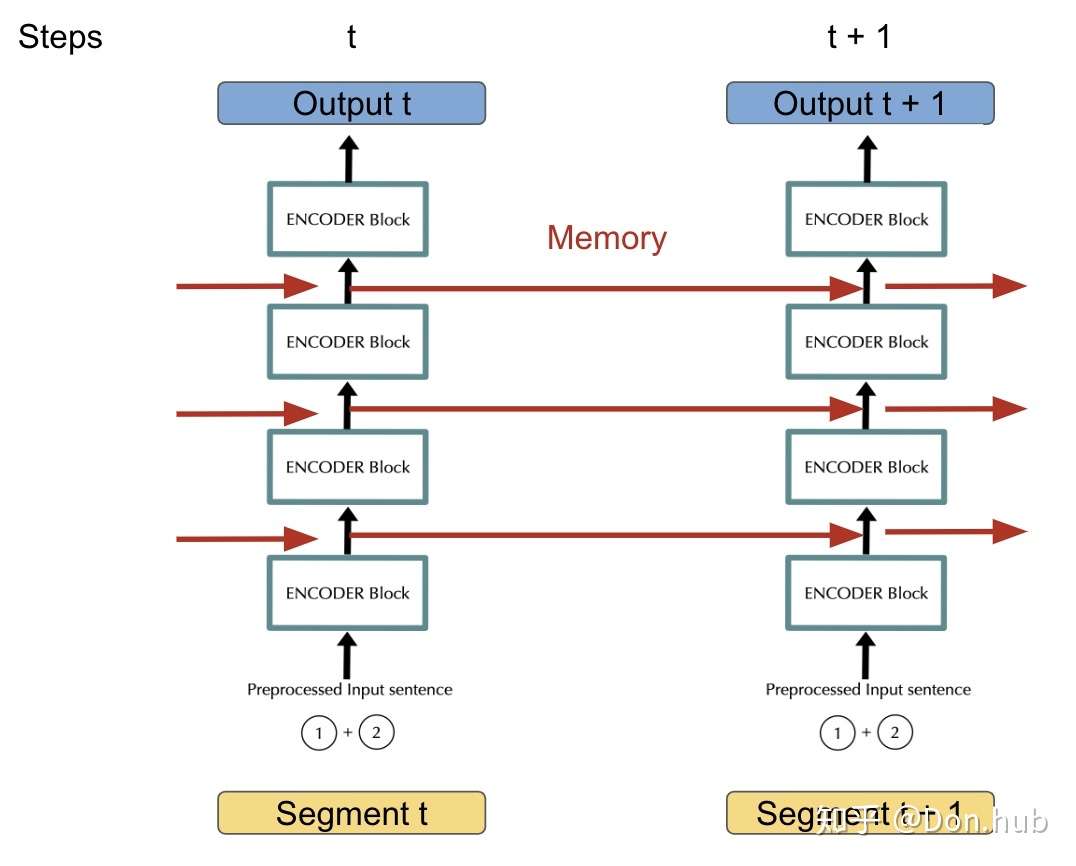
 具体的过程中，加入segment t生成的memory为(prev_seq_len, batch_size, d_model), segment t+1进行运算的时候，对于其key和value，由于这两个状态编码了token的信息，因而需要look ahead来混合t时刻的信息，做法就是在进行multihead的时候，不是针对当前时刻的输入x(cur_seq_len, batch_size, d_model)进行project(x)，而是进行project(concat([memory, x], axis=0))（project一般为Linear层），另外，memory不参与本segment的反响传播。

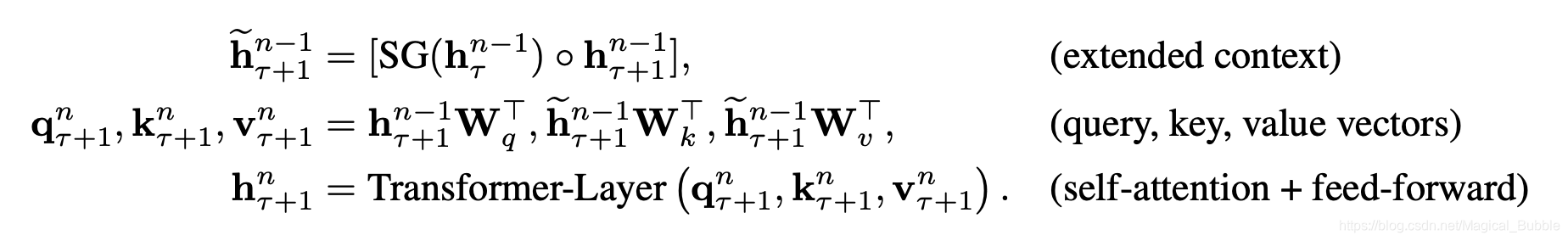
 其中，τ表示第几段，n表示第几层，h表示隐层的输出。SG(⋅)表示停止计算梯度，$[ h u ∘ h v ]$ 表示在长度维度上的两个隐层的拼接，W.是模型参数。

 transformer-xl中还有个需要注意的地方就是，其使用的不是absolute positional encoding，因为在分段的情况下，如果仅仅对于每个段仍直接使用Transformer中的位置编码，即每个不同段在同一个位置上的表示使用相同的位置编码，就会出现问题。比如，第i−2段和第i−1段的第一个位置将具有相同的位置编码，但它们对于第i段的建模重要性显然并不相同（例如第i−2段中的第一个位置重要性可能要低一些）。因此，需要对这种位置进行区分。取而代之的是，transformer-xl使用的是relative position encoding技术，其提出理论基础如下： \(\begin{aligned} (QK^{T})_{i,j}&=(E+P)_{i,\circ}W^{Q}(W^{K})^{T}(E+P)^{T}_{\circ,j}\\&=(E+P)_{i,\circ}W^{Q}(W^{K})^{T}(E^{T}+P^{T})_{\circ,j}\\&=E_{i,\circ}W^{Q}(W^{K})^{T}(E^{T}+P^{T})_{\circ,j}+P_{i,\circ}W^{Q}(W^{K})^{T}(E^{T}+P^{T})_{\circ,j}\\&=\underbrace{E_{i,\circ}W^{Q}(W^{K})^{T}E^{T}_{\circ,j}}_{a}++\underbrace{P_{i,\circ}W^{Q}(W^{K})^{T}P^{T}_{\circ,j}}_{b}+\underbrace{E_{i,\circ}W^{Q}(W^{K})^{T}P^{T}_{\circ,j}}_{c}+\underbrace{P_{i,\circ}W^{Q}(W^{K})^{T}E^{T}_{\circ,j}}_{d} \end{aligned}\)  其中E为token的embeddings，P为positional embeddings，这俩均是经过了extend，添加上了上一个segment的memory信息。从上面的公式来看，主要分了4项：

1. a 项没有包含 位置信息，代表的是在第 行的字应该对第 列的字提供多大的注意力。
2. b 项捕获的是模型的global attention，指的是一个字在position 应该要对 position 付出多大的注意力。
3. c 项在捕获的是position i处的字对于position j的注意力的程度。
4. d 项是c项的逆序。

 上面的展开其实是transformer 的展开，transformer-xl做了如下的改进： \(\begin{aligned} &替换b,c,d项\\ &b:P_{i,\circ}W^{Q}(W^{K})^{T}P^{T}_{\circ,j}\mapsto \mu(W^{R})^{T}P_{\circ,i-j}^{T}\\&c:E_{i,\circ}W^{Q}(W^{K})^{T}P^{T}_{\circ,j} \mapsto E_{i,\circ}W^{Q}(W^{R})^{T}P_{\circ,i-j}^{T}\\&d: P_{i,\circ}W^{Q}(W^{K})^{T}E^{T}_{\circ,j} \mapsto \nu(W^{K})^{T}E_{\circ,j}^{T}\\&最终得到:\\&(QK^{T})_{i,j}=E_{i,\circ}W^{Q}(W^{K})^{T}E^{T}_{\circ,j}+\mu(W^{R})^{T}P_{\circ,i-j}^{T}+E_{i,\circ}W^{Q}(W^{R})^{T}P_{\circ,i-j}^{T} +\nu(W^{K})^{T}E_{\circ,j}^{T} \end{aligned}\)  对比来看，主要有3点变化（集中在键的相对位置及尤其引起的其他变化）：

• b,c两项中，将所有绝对向量$P_{i}$转为相对位置向量$P_{i-j}$，和vanilla Transformer一样，这是个固定的编码向量，不需要学习。
• d项，将查询的$P_{i,\circ}W^{Q}$向量转为一个需要学习的参数向量，因为在考虑相对位置的时候，不需要查询绝对位置，因此对于任意的，都可以采用同样的向量。同理，在b这一项中，也将查询的$P_{i,\circ}W^{Q}$向量转为另一个需要学习的参数向量，区分对待主要是和第3点结合。
• 将键的权重变换矩阵分为和两个矩阵，分别得到content-based的键向量、location-based的键向量，更加细致。

 在新的计算形式下，每一项都有了更加直观的意义，如下：

• 表示基于内容的寻址，即没有考虑位置编码的原始分数
• 表示全局的位置偏置，从相对位置层面衡量键的重要性
• 表示内容相关的位置偏差，即相对于当前内容的位置偏差
• 表示全局的内容偏置，从内容层面衡量键的重要性

⚠️：relative positional encoding在工程层面有个trick，可去原文的appendix B查看。

工程实现图示，有助于工程实现的理解

 最终，transformer-xl相比于transformer取得了明显的提升：

• Transformer-XL学习的依赖项比RNNs长80%左右，比最初的transformer长450%，最初的transformer通常比RNNs具有更好的性能，但由于上下文的长度固定，不是远程依赖项建模的最佳选择
• 在评估语言建模任务时，ransformer-XL的速度比vanilla transformer快1800多倍，因为不需要重新计算。
• 由于有更好长距离依赖建模，Transformer-XL在长序列上具有更好的perplexity性能(更准确地预测样本)；而且通过解决上下文碎片问题，它在短序列上也有更好的性能。

2.3 Reformer

 ICLR 2020论文，致力于解决解决transformer的对资源的饥渴需求问题，标准的transformer有效率方面有着比较大的问题：

• transformer单层的参数在5亿个，需要内存约2GB；每一层的激活结果，假如序列大小为 64K ， embedding size是1024，batch size是8，共计64k *1k *8=5亿个floats，又需要2GB的内存。如果多层叠加起来，对于资源的消耗是非常惊人的。
• Transformer每一层中间的前馈全连接网络的维度$d_{ff}$要比注意力层的$d_{model}$大的多，所以消耗的内存更多。
• 序列长度为L的attention在时间和空间的复杂度都是$O(L^{2})$，所以如果序列过大，很容易就出现OOM的问题。

 针对上面的问题，Reformer通过三个改进来加以解决：

• Reversible layers，只需要存储一层的激活结果即可，N的因素消失了。

 使用Reversible residual Network (RevNet)，其思想是每一层的activations可以根据下一层的activations推导获得，从而不需要在内存中储存activations。在原本的residual layer中，由公式输出得到activations。其中F是residual 函数。在RevNet中，先将输入分为两个部分和，然后通过不同residual functions： 和 得到输出和：

 再根据以下结构，从输出获得输入：

 将可逆残差网络的思想应用到Transformer中，在可逆块中结合了自注意力层和前馈网络层。结合上面的可逆残差公式，F函数变成了自注意力层，G函数变成了前馈网络层，注意的是每层的归一化处理放在了残差块里面。

 如此，使用可逆的Transformer在每一层中就无需存储激活值，也就避免了这一项。可逆层代替标准的残差层，可以在训练过程中只存储一次激活，而不是$N$次。

• 分块计算前馈全连接层，节省内存。

 每一层Transformer中前馈网络所用的中间向量维度$d_{ff}=4k$甚至更高维度，依然非常占用内存；然而，一个序列中各个tokens在前馈网络层的计算是相互独立的，所以这部分计算可以拆分为c个组块以降低内存的使用。虽然该操作其实可并行处理，但是每次只计算一个chunk，通过时间换取内存空间:

• 采用局部敏感哈希(Locality-Sensitive Hashing, LSH)技术，近似计算注意力，将时空开销从$O(L^{2})$变为$O(LlogL)$。

 标准transformer中，记忆力计算公式为： \(Attention(Q,K,V) = softmax(\frac {QK^{T}}{\sqrt[]{d_{k}}})V\) 而Softmax下其实有很多的值被置为了0，有价值的$q_{i}k_{j}^{T}$往往是非常少的，所以完全不需要计算全量的$QK^{T}$，只需要计算与query最想干的若干个key即可。而如何选择最想干的那些key呢？

 答案就是LSH，其基本思路是距离相近的向量能够很大概率hash到一个桶内，而相距较远的向量hash到一个桶内的概率极低。

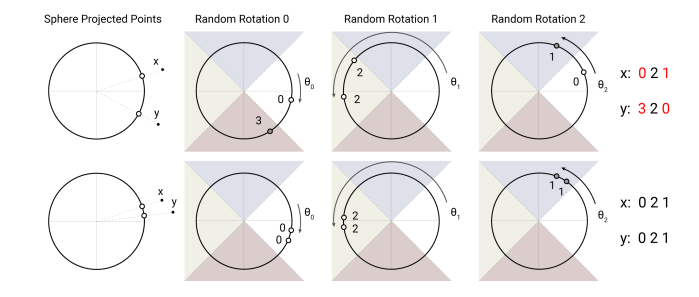
 formally，LSH attention的计算流程如下：

 改写公式(3): \(o_{i}=\sum_{j \in P_{i}}exp(q_{i}*k_{j}-z(i,P_{i}))v_{j}\quad where\ P_{i}={j:i \ge j}\)  $P_{i}={j:h(q_{i})=h(k_{j})}$就是位置$i$的query需要关注的tokens集合，$h$代表$hash$函数，$z$表示分区函数（即$softmax$中的规格化项，相当于$softmax$中的分母），为了简便，这里省去了$\sqrt[]{d_{k}}$ 。

 为了便于批计算，在整个序列上做个修改，$\widetilde{P_{i}}={0,1,,…,l}\supseteq P_{i}$使用如下修正公式： \(o_{i}=\sum_{j \in \widetilde{P_{i}}} exp(q_{i}*k_{j}-m(j,P_{i})-z(i,P_{i}))v_{j}\quad where \, m(j,P_{i})=\begin{cases}&\infty\quad if\,j \notin P_{i} \\&0\quad otherwise\end{cases}\)  即对于不能attend到的位置，为正无穷，那么减去正无穷再去exp操作，其结果为0。相当于mask掉了,这样就不需要对于每个位置i都有单独的.

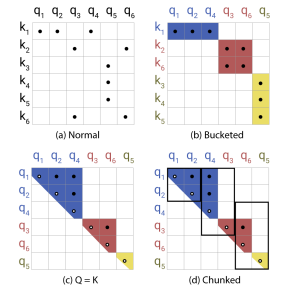
 图a：常规的attention机制中，黑点代表的是softmax中占主导的位置。注意这边的attention使用的是encoder的attention， 否则 无法attend to 。另外，这种全attention(即encoder中的attention)的attention矩阵一般是稀疏的，但计算中并没有利用这种稀疏性，所以可以利用这个降低时间空间复杂度。

 图b：计算query和key所归属的hash桶。再按照桶进行排序，同一个桶又按照原本的位置进行排序得到图b。可以看到，同一个桶，可以出现多个query但keys很少的情况，例如图中蓝色的桶query有3个，都attend到同一个key中。由于相似的item很有可能落在同一个桶里，所以只在每个桶内部进行attention就可以近似全attention。

 图d: 即使Q=K，还是会出现一个问题：有的桶中个数多，有的桶中个数少。比如一个极端情况，2个桶，其中一个桶占据了所有的keys，另一个桶为空，那么LSH attention就没有起作用。于是在图c的基础上，增加了chunk的操作。对输入进行排序之后(即图c中先桶排序，同个桶内按照token 的 position排序）得到新的序列顺序，比如图中原来的序列顺序是，新的序列顺序是 。每个chunk内query的上限个数为, ( 为输入query的长度) ，每个桶平均大小为，这里假设桶中数量增加到均值两倍的概率足够低。对于桶中的每个query，都可以attend to自己以及前一个桶中相同hash 值的key。

 单个hash函数，总不可避免的会出现个别相近的items却被分到不同的桶里，多轮$hash \ {h(1),h(2),…}$可以减少这种情况的发生： \(P_{i}=\bigcup_{r=1}^{n_{rounds}}P_{i}^{(r)}\quad where \ P_{i}^{(r)}=\{j:h^{(r)}(q_{i})=h^{(r)}(q_{j})\}\)

def make_unit_length(x, epsilon=1e-6):
  	'''
  	k_{j}=\frac{q_{j}}{ ||q_{j}||}
  	对query_{j}归一化得到key_{j},确保可以映射到同一个桶中,要注意这里是针对每个桶内做softmax(QK^{T})的。
  	:param x: [batch_size, n_hashes*n_buckets, bucket_size, emb]
  	'''
    norm = x.norm(p=2, dim=-1, keepdim=True)
    return x.div(norm + epsilon)

def sort_key_val(t1, t2, dim=-1):
    values, indices = t1.sort(dim=dim)
    t2 = t2.expand_as(t1)
    return values, t2.gather(dim, indices)

def batched_index_select(values, indices):
    last_dim = values.shape[-1]
    return values.gather(1, indices[:, :, None].expand(-1, -1, last_dim))
class LSH_Attention(nn.Module):
	'''LSH attention的实现'''
      def __init__( self,
                  dropout = 0.,
                  bucket_size = 64,
                  n_hashes = 8,
                  attend_across_buckets = True,
                  drop_for_hash_rate = 0.0):
        '''
        :param attend_across_buckets：是否允许跨桶attend
        '''
        super().__init__()

        if dropout >= 1.0:
            raise ValueError('Dropout rates must be lower than 1.')

        self.dropout = nn.Dropout(dropout)
        self.dropout_for_hash = nn.Dropout(drop_for_hash_rate)

        self.n_hashes = n_hashes
        self.bucket_size = bucket_size

        self._attend_across_buckets = attend_across_buckets

    def _sample_rotation(self, shape, vecs):
      	'''
      	随机旋转的矩阵
      	:param vecs: [batch_size, seqlen, emb]
      	'''
        device = vecs.device
        return torch.randn(shape, device=device)

    def hash_vectors(self, n_buckets, vecs):
        batch_size = vecs.shape[0]   
        device = vecs.device

        assert n_buckets % 2 == 0

        rot_size = n_buckets

        rotations_shape = (
            vecs.shape[-1],
            self.n_hashes,
            rot_size // 2)

        random_rotations = self._sample_rotation(rotations_shape, vecs)

        dropped_vecs = self.dropout_for_hash(vecs)
        # 随机旋转，rotated_vecs的shape为[batch_size, n_hashes,seqlen, rot_size//2],代表每一轮hash的序列被分到的桶
        rotated_vecs = torch.einsum('btf,fhi->bhti', dropped_vecs, random_rotations)

        rotated_vecs = torch.cat([rotated_vecs, -rotated_vecs], dim=-1)
        # buckets： [batch_size, n_hashes, seqlen]
        buckets = torch.argmax(rotated_vecs, axis=-1)  
        # 为每一轮的hash添加不同的offset，确保不同hash轮数的桶编号不会重叠。
        offsets = torch.arange(self.n_hashes, device=device)
        offsets = torch.reshape(offsets * n_buckets, (1, -1, 1))
        buckets = torch.reshape(buckets + offsets, (batch_size, -1,))
        

        return buckets

    def forward(self, qk, v):
        batch_size, seqlen, _ = qk.shape  
        device = qk.device

        n_buckets = seqlen // self.bucket_size
        n_bins = n_buckets

        buckets = self.hash_vectors(n_buckets, qk)
        # We use the same vector as both a query and a key.
        assert int(buckets.shape[1]) == self.n_hashes * seqlen
        ticker = torch.arange(0, self.n_hashes * seqlen, device=device).unsqueeze(0)
        # 为桶内word加上编号，以实现先按桶排序，内部再按照词排序
        buckets_and_t = seqlen * buckets + (ticker % seqlen) 
        buckets_and_t = buckets_and_t.detach()

        # sticker标识排序后的下标索引
        sbuckets_and_t, sticker = sort_key_val(buckets_and_t, ticker, dim=-1)
        # 这里对sticker进行重新排序，以便恢复序列的输入顺序
        _, undo_sort = sort_key_val(sticker, ticker, dim=-1)

        sbuckets_and_t = sbuckets_and_t.detach()
        sticker = sticker.detach()
        undo_sort = undo_sort.detach()

        st = (sticker % seqlen)  
        sqk = batched_index_select(qk, st)
        sv = batched_index_select(v, st)

        # Split off a "bin" axis 以便chunk内部进行attention计算
        bq_t = bkv_t = torch.reshape(st, (batch_size, self.n_hashes * n_bins, -1))
        bqk = torch.reshape(sqk, (batch_size, self.n_hashes * n_bins, -1, sqk.shape[-1]))
        bv = torch.reshape(sv, (batch_size, self.n_hashes * n_bins, -1, sv.shape[-1]))
        bq_buckets = bkv_buckets = torch.reshape(sbuckets_and_t // seqlen, (batch_size, self.n_hashes * n_bins, -1))

        # Hashing operates on unit-length vectors. Unnormalized query vectors are
        # fine because they effectively provide a learnable temperature for the
        # attention softmax, but normalizing keys is needed so that similarity for
        # the purposes of attention correctly corresponds to hash locality.
        bq = bqk
        bk = make_unit_length(bqk)

        # Allow each chunk to attend within itself, and also one chunk back. Chunk
        # boundaries might occur in the middle of a sequence of items from the
        # same bucket, so this increases the chances of attending to relevant items.
        def look_one_back(x):
            x_extra = torch.cat([x[:, -1:, ...], x[:, :-1, ...]], dim=1)
            return torch.cat([x, x_extra], dim=2)

        bk = look_one_back(bk)
        bv = look_one_back(bv)
        bkv_t = look_one_back(bkv_t)
        bkv_buckets = look_one_back(bkv_buckets)

        # Dot-product attention.
        dots = torch.einsum('bhie,bhje->bhij', bq, bk) / (bq.shape[-1] ** -0.5)

        # Causal masking， 屏蔽掉后面的word
        mask = bq_t[:, :, :, None] < bkv_t[:, :, None, :]
        dots = dots - 1e9 * mask

        # Mask out attention to self except when no other targets are available.
        self_mask = bq_t[:, :, :, None] == bkv_t[:, :, None, :]
        dots = dots - 1e5 * self_mask

        # Mask out attention to other hash buckets.
        if not self._attend_across_buckets:
            bucket_mask = bq_buckets[:, :, :, None] != bkv_buckets[:, :, None, :]
            dots = dots - 1e7 * bucket_mask

        # Softmax.
        dots_logsumexp = torch.logsumexp(dots, dim=-1, keepdim=True)
        dots = torch.exp(dots - dots_logsumexp)
        dots = self.dropout(dots)

        bo = torch.einsum('buij,buje->buie', dots, bv)
        so = torch.reshape(bo, (batch_size, -1, bo.shape[-1]))
        slogits = torch.reshape(dots_logsumexp, (batch_size, -1,))

        o = batched_index_select(so, undo_sort)
        _, logits = sort_key_val(sticker, slogits, dim=-1)

        if self.n_hashes == 1:
            out = o
        else:
            o = torch.reshape(o, (batch_size, self.n_hashes, seqlen, o.shape[-1]))
            logits = torch.reshape(logits, (batch_size, self.n_hashes, seqlen, 1))
            probs = torch.exp(logits - torch.logsumexp(logits, dim=1, keepdims=True))
            out = torch.sum(o * probs, dim=1)

        assert out.shape == v.shape
        return out
      
class LSHSelfAttention(nn.Module):
      def __init__(self, emb, heads = 8, bucket_size = 64, n_hashes = 8, **kwargs):
      '''
      :param emb: embedding_size
      :param heads: 同标准transformers
      :param bucket_size: 桶容量，即每个桶包含的word的数目
      :param n_hashes: hash轮数
      '''
        super().__init__()
        self.heads = heads

        self.toqk = nn.Linear(emb, emb * heads)
        self.tov = nn.Linear(emb, emb * heads)
        self.unify_heads = nn.Linear(emb * heads, emb)

        self.bucket_size = bucket_size
        self.lsh_attn = LSHAttention(bucket_size=bucket_size, **kwargs)

    def forward(self, x):
        b, t, e, h = *x.shape, self.heads
        assert t % self.bucket_size == 0, f'Sequence length needs to be divisible by target bucket size - {self.bucket_size}'

        qk = self.toqk(x)
        v = self.tov(x)

        def merge_heads(v):
            return v.view(b, t, h, e).transpose(1, 2).reshape(b * h, t, e)

        def split_heads(v):
            return v.view(b, h, t, e).transpose(1, 2).contiguous()

        qk = merge_heads(qk)
        v = merge_heads(v)
        attn_out = self.lsh_attn(qk, v)
        out = split_heads(attn_out).view(b, t, h * e)

        return self.unify_heads(out)

• axial positional encoding

  ⚠️：这个技术并没有在paper中详述，而是在代码中做了实现。

 在标准transformer中，使用positional encoding来编码位置信息，这里其实也是一种embedding技术，将每个位置编码为一个向量，所以其shape为¥¥$[max_seq_len, hidden_size]$,简写为$[n_{max}, d_{h}]$,位置编码表示为$E=[e_{1},…,e_{n_{max}}]$.

 假定$d_{h}=4,n_{max}=49,E$图示如下，矩形高度为$d_{h}$：

 如果训练一个词表大小为$0.5M,hidden_size=1024$的positional encoding，那么需要的参数约为0.5𝑀×1024∼512𝑀，需要的内存空间约为2GB，这显然是比较大的。

 Reformer的作者则是通过因式分解$n_{max}$及切分$d_{h}$来大幅度缩减了内存需求。用户可以通过设定$axial_pos_shape$参数声明一个包含两个值的list：$n_{max}^{1},n_{max}^{2}$使得$n_{max}^{1}*n_{max}^{2}=n_{max}$,通过设定$axial_pos_embds_dim$参数声明一个包含两个值的list：$d_{h}^{1},d_{h}^{2}$使得$d_{h}^{1}+d_{h}^{2}=d_{h}$.

 举个例子说明一下流程，假如$axial_pos_shape=[n_{max}^{1}=7,n_{max}^{2}=7]$:

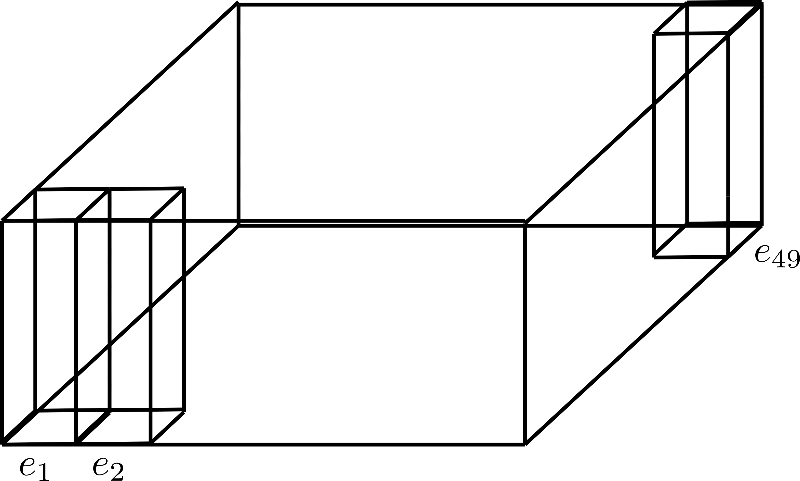
 上图的三个棱柱代表对应的encoding vectors，不过可以注意到，49个encoding vectors被分解成了一个7*7的矩阵，现在要做的就是使用一行的7个encoding vectors去拓展出其他的6行，基本上是重复使用他们的值。因为不鼓励不同的编码向量有相同的值，所以每一个维度（也就是高度$d_{h}$）被切分为size =1 的lower encoding vector $e_{down}$和size=3的upper encoding vector $e_{up}$，这样的话lower 部分可以沿着行维度拓展而upper部分沿着列维度拓展：

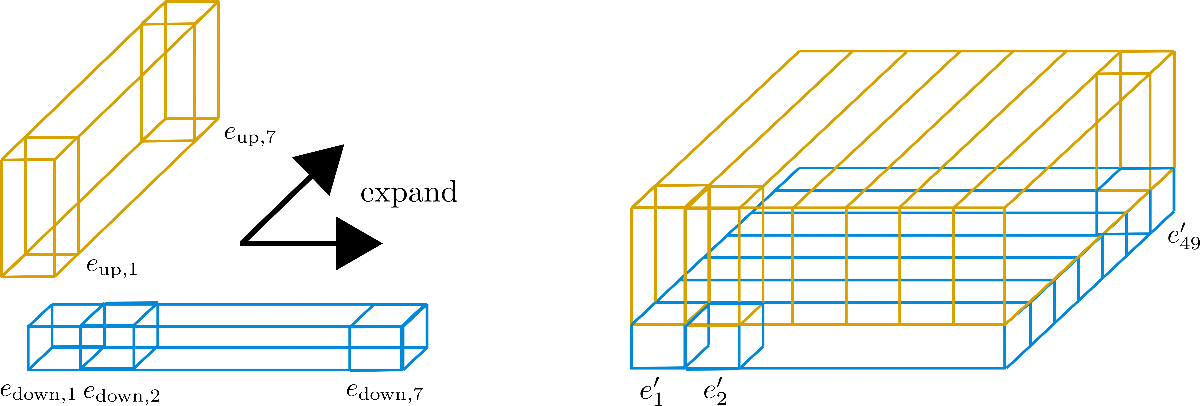
 现在，对于”sub”-vectors $E_{down}=[e_{down,1},…,E_{down,49}]$只有第一行的7个元素被保留，然后沿着列维度拓展，相反，对于”sub”-vectors $E_{up}=[e_{up,1},…,e_{up,49}]$,同样只有第一列的7个元素被保留，然后沿着行维度拓展，得到的embedding vectors $e_{i}^{‘}$为： \(e_{i}^{'}=\begin{bmatrix} e_{down,i\%n_{max}^{1}}\\ e_{up,[\frac {i}{n_{max}^{2}}]} \end{bmatrix}\)  现在，这个新的encodings $E^{‘}=[e_{1}^{‘},…,e^{‘}{n{max}}]$就被称为Axial Position Encodiings，更详细的计算图如下：

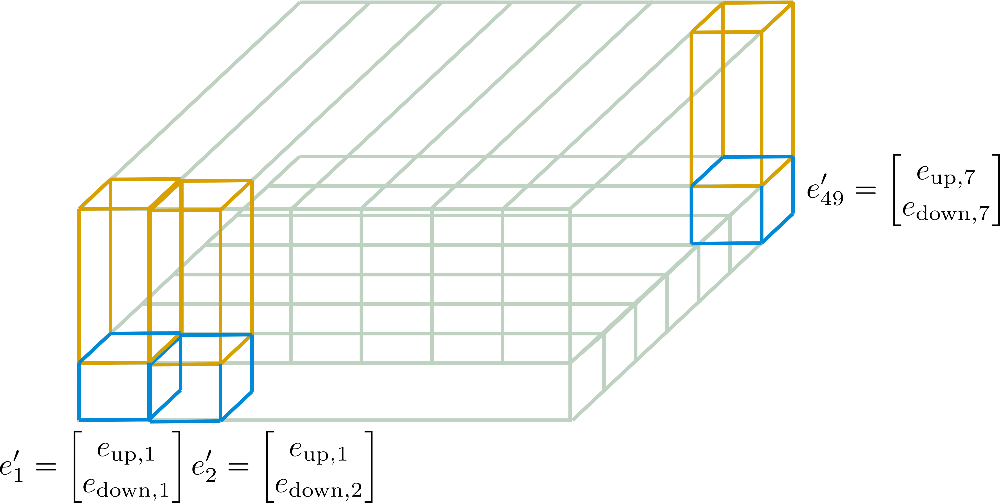
 这里要看到的关键是，axial position encoding通过设计确保所有向量$[e_{1}^{‘},…,e_{n_{max}}^{‘}]$都不相等，如果axial position encoding被模型学习到，那么模型就可以更灵活地学习高效的位置表示。通过axial position encoding技术，可以估算一下内存节省的效率，假如$axial_pos_shape=[1024,512]$,$axial_pos_embds_dim=[512,512],$处理的tokens数目为$0.5M$, 对于Reformer模型，其参数数目为1024×512+512×512∼800𝐾，大约对应$3MB$内存，大大缩减了内存需求量。

• Previous
  强大的transformer
• Next
  nlp领域的巧妙trick